Exterior Angles
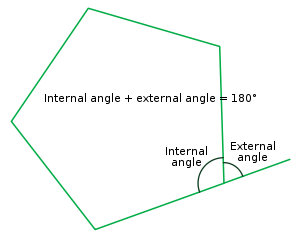
Exterior Angle is the angle between any side of a shape and a line extended from the next side. The sum of the external angles of any polygon is 360°. A polygon has one internal angle per vertex.
Exterior Angle of a Triangle: In a triangle, the exterior angle is formed when one side of the triangle is extended. The straight angle outside the triangle, but adjacent to an interior angle is called as an exterior angle of the triangle.
Exterior angle of a vertex = 180 - interior angle.
Difference Between Interior and Exterior Angles
Exterior Angle of a Triangle: In a triangle, the exterior angle is formed when one side of the triangle is extended. The straight angle outside the triangle, but adjacent to an interior angle is called as an exterior angle of the triangle.
Exterior angle of a vertex = 180 - interior angle.
Difference Between Interior and Exterior Angles
The sum of all the internal angles of a polygon is calculated by 180(n-2) where n is the number of sides.
Sum of all the internal angles of a pentagon is 540 degrees .
180(n − 2) = 180(5 − 2) = 180(3) = 540.
Angle of each side is 108 degree.
540/5=108
So external angle= 180-108 = 72 degrees
The sum of the external angle on the same vertex is equal to 180°.
The parallel case: If a transversal cuts across the parallel lines, then the alternate exterior angles will have the same measure.
The non-parallel case: If a transversal cuts across non-parallel lines, then the Alternate Exterior Angles will have no relationship to each other. Each angle may be simply the alternate angle to the other.
Example Problems on Exterior Angles
Example Problem 1:
Solve the exterior angles of x.
Solution:
Sum of all the internal angles of a pentagon is 540 degrees .
180(n − 2) = 180(5 − 2) = 180(3) = 540.
Angle of each side is 108 degree.
540/5=108
So external angle= 180-108 = 72 degrees
The sum of the external angle on the same vertex is equal to 180°.
The parallel case: If a transversal cuts across the parallel lines, then the alternate exterior angles will have the same measure.
The non-parallel case: If a transversal cuts across non-parallel lines, then the Alternate Exterior Angles will have no relationship to each other. Each angle may be simply the alternate angle to the other.
Example Problems on Exterior Angles
Example Problem 1:
Solve the exterior angles of x.
Solution:
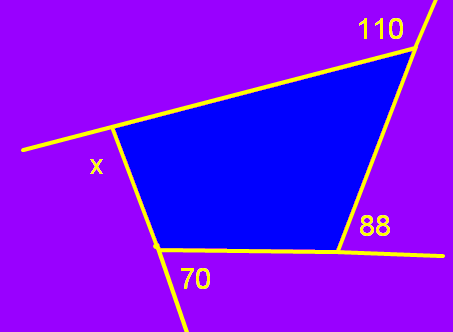
Sum of the exterior angles of a figure is 360 degrees.
Add each exterior angle and equate to the 360 degrees.
In the given figure, the exterior angles are 88, x, 70, 110 degrees.
88+70+110+x=360
268+x=360
X=360-268
X=92 degrees.
My previous blog post was on neet 2014 syllabus please express your views on the post by commenting.
Example Problem 2:
Solve the exterior angles of x.
Add each exterior angle and equate to the 360 degrees.
In the given figure, the exterior angles are 88, x, 70, 110 degrees.
88+70+110+x=360
268+x=360
X=360-268
X=92 degrees.
My previous blog post was on neet 2014 syllabus please express your views on the post by commenting.
Example Problem 2:
Solve the exterior angles of x.
Solution:
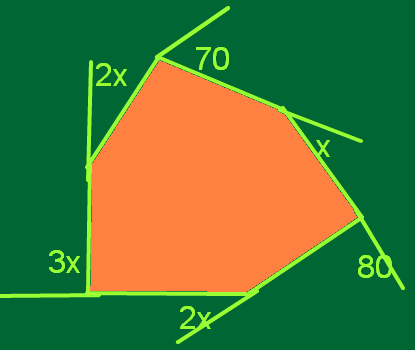
Sum of exterior angles of a figure is 360 degrees.
Add each exterior angle and equate to the 360 degrees.
Given figure exterior angles are 70, 2x, 2x, 80, 3x degrees.
70+80+2x+2x+3x=360
150+7x=360
7x=210
X=30
2x=2*30=60
3x=90
Each exterior angle is 70°, 60°, 60°, 90°, and 80° degrees.
Sum of exterior angles of a figure is 360 degrees.
Add each exterior angle and equate to the 360 degrees.
Given figure exterior angles are 70, 2x, 2x, 80, 3x degrees.
70+80+2x+2x+3x=360
150+7x=360
7x=210
X=30
2x=2*30=60
3x=90
Each exterior angle is 70°, 60°, 60°, 90°, and 80° degrees.